
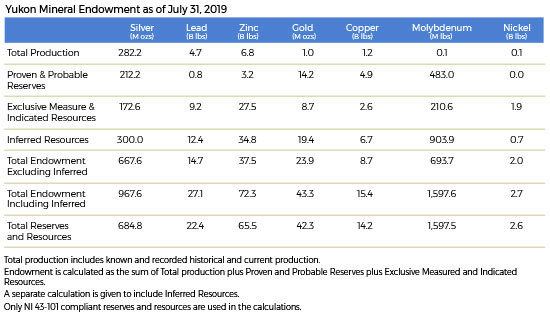
Yukon Mineral Resource Endowment
The Yukon has a long history of mineral exploration dating back to August 1896 with the beginning of the Klondike Gold Rush. Since then, other mining areas including Faro, Keno Hill and Whitehorse to name a few, have produced significant amounts of silver, lead, zinc, copper and gold.
The Yukon currently has two producing mines. The Eagle Gold Mine, owned by Victoria Gold Corp, is the newest mine with the first gold pour on September 17, 2019. The Minto Mine, owned by Minto Explorations (subsidiary of Pembridge Resources plc), resumed copper, silver and gold production.
There are another 51 deposits that have reported NI 43-101 compliant resources.
Silver Endowment
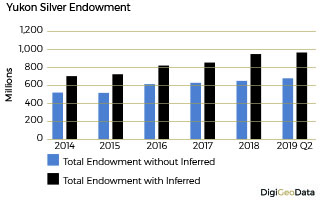
Silver endowment as of July 31, 2019 for the Yukon not including inferred resources is 667.6 million ounces. Adding the inferred resources of 300 million ounces increases total endowment to 967.6 million ounces.
Prior to 2014, historical silver production was 281.9 million ounces. Most of the historical silver production prior to 2014, was produced in the Keno Hill mining camp. The top silver producer was the Hector-Calument mine with over 96 million ounces. The most recent production came from the Minto mine with aggregated silver production from 2007 to 2018 of 2.3 million ounces.
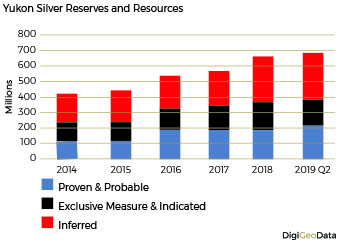
At the end of Q2 2019, proven and probable silver reserves were calculated at 212.2 million ounces. In the same period, exclusive measured and indicated resources were 172.6 million ounces and inferred resources were 300 million ounces.
Total silver resources increased 63% from 419.5 million ounces in 2014 to just over 684.9 million ounces by the end of Q2 2019.
Lead Endowment
Lead endowment as of July 31, 2019 for the Yukon not including inferred resources is 14.7 billion pounds. Adding the inferred resources of 12.4 billion pounds increases total endowment to 27.1 billion pounds.
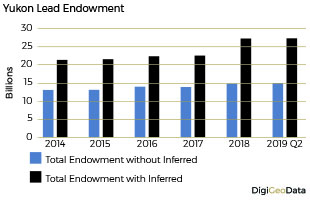
Historical lead production prior to 2014 was 4.7 billion pounds. The Faro mine, one of the largest open pit lead-zinc mines in the world, produced most of the lead in the Yukon at 3.9 billion pounds (83%). The next most significant producer was the Hector-Calument mine in the Keno Hill mining camp with 406.9 million pounds.
The most recent production came from the Bellekeno mine (2011-2013) and the Wolverine mine (2013).
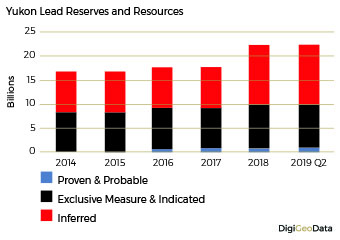
Proven and probable lead reserves at the end of Q2 2019 were 806 million pounds. Exclusive measured and indicated resources calculated to 9.2 billion pounds with inferred resources of 12.4 billion pounds.
Total lead resources increased by close to 25% from 16.6 billion pounds in 2014 to 22.4 billion pounds by the end of Q2 2019.
Zinc Endowment
Zinc endowment as of July 31, 2019 for the Yukon not including inferred resources is 37.5billion pounds. Adding the inferred resources of 34.8 billion pounds increases total endowment to 72.3 billion pounds.
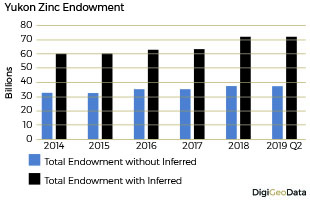
Historical zinc production prior to 2014 was 6.8 billion pounds. The Faro mine, one of the largest open pit lead-zinc mines in the world, produced most of the zinc in the Yukon at 5.9 billion pounds (88%). The next two largest significant zinc producers were the Vangorda mine also in the Faro mining camp with 349 million pounds and the Hector-Calument mine in the Keno Hill mining camp with 334 million pounds. The most recent production came from the Bellekeno mine (2011-2013) and the Wolverine mine (2013).
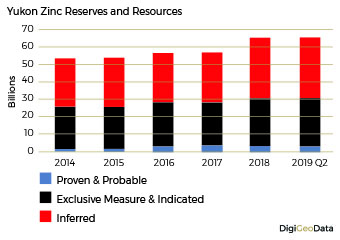
Proven and probable zinc reserves at the end of Q2 2019 were 3.2 billion pounds. Exclusive measured and indicated resources calculated to 27.6 billion pounds with inferred resources of 34.8 billion pounds.
Total zinc resources increased by over 22% from 53.6 billion pounds in 2014 to 65.5 billion pounds by the end of Q2 2019.
Gold Endowment
Gold endowment as of July 31, 2019 for the Yukon not including inferred resources is 23.9 million ounces. Adding the inferred resources of 19.4 million ounces increases total endowment to 43.3 million ounces.
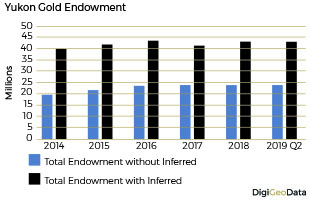
Prior to 2014, historical silver production was 941.1 million ounces. Most of the historical gold production prior to 2014, was produced at the Brewery Creek mine (1996–2000) calculated at 276,700 ounces and the Whitehorse Copper mine (1967-19820 at 250,000 ounces.
The most recent production came from the Minto mine with aggregated gold production from 2007 to 2018 with 245,400 ounces.
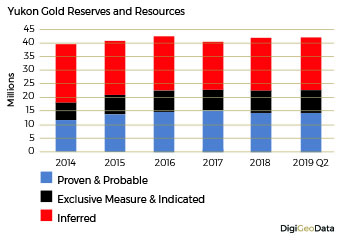
At the end of Q2 2019, proven and probable gold reserves were calculated at 14.2 million ounces. In the same period, exclusive measured and indicated resources were 8.7 million ounces and inferred resources were 19.4 million ounces.
Total gold resources increased by close to 8% from 39.3 million ounces in 2014 to 42.3 million ounces by the end of Q2 2019.
Copper Endowment
Copper endowment as of July 31, 2019 for the Yukon not including inferred resources is 8.7 billion pounds. Adding the inferred resources of 6.7 billion pounds increases total endowment to 15.4 billion pounds.
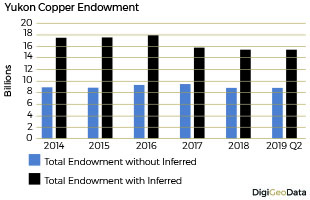
Historical copper production prior to 2014 was 962.2 million pounds. The Whitehorse Copper mine (1967-1982), produced 271.5 million pounds. Prior to 2014, the Minto mine produced 690.7 million pounds from 2007 to 2013. From 2014 to the end of 2018, the Minto mine produced another 182.3 million pounds. Total production for the Minto mine is 873 million pounds, accounting for almost 91% of the total copper production in the Yukon as of July 31, 2019.
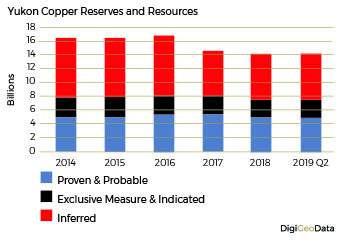
Proven and probable copper reserves at the end of Q2 2019 were 4.9 billion pounds. Exclusive measured and indicated resources calculated to 2.6 billion pounds with inferred resources of 6.7 billion pounds.
Total copper resources decreased by 15% from 16.5 billion pounds in 2014 to 14.2 billion pounds by the end of Q2 2019.
This was largely due to the re-stating of inferred copper resources at the Nickel Shaw deposit from 2.6 billion pounds in 2015 to 312 million pounds in 2017.
Other Mineral Endowments
The Yukon has other commodities that have been and/or are being actively explored. Some of these minerals are highlighted below.
Molybdenum
Molybdenum endowment as of July 31, 2019 for the Yukon not including inferred resources is 693.7 million pounds. Adding the inferred resources of 903.9 million pounds increases total endowment to 1.6 billion pounds.
Nickel
Nickel endowment as of July 31, 2019 for the Yukon not including inferred resources is 2.0 billion pounds. Adding the inferred resources of 0.7 billion pounds increases total endowment to 2.7 billion pounds.
Cobalt
Cobalt endowment as of July 31, 2019 for the Yukon not including inferred resources is 107 million pounds. Adding the inferred resources of 38 million pounds increases total endowment to 145 million pounds.
Platinum
Platinum endowment as of July 31, 2019 for the Yukon not including inferred resources is 2.6 million ounces. Adding the inferred resources of 0.9 million ounces increases total endowment to 3.5 million ounces.
Palladium
Palladium endowment as of July 31, 2019 for the Yukon not including inferred resources is 2.6 million ounces. Adding the inferred resources of 0.9 million ounces increases total endowment to 3.6 million ounces.
Tungsten
Tungsten endowment as of July 31, 2019 for the Yukon not including inferred resources is 1.2 billion pounds. Adding the inferred resources of 900 million pounds increases total endowment to 2.1 billion pounds.
November 25, 2019